
Здравствуйте, дорогие товарищи! Перед вами 5-й выпуск из цикла «диамат, истмат и физмат». Сегодня, пожалуй, будет преобладать третья составляющая. И пожалуй, мне следует заранее извиниться перед лириками, что физики, быть может, будет многовато, а перед физиками – что изложена она будет чресчур вольно. И всё же… В современные т. н. «популярные» издания из теоретической физики просачиваются, как правило, исключительно вульгарные интерпретации её положений, не приближающие читателя или зрителя к их пониманию, а создающие у него лишь некую иллюзию причастности к науке.

А между тем нам следует научиться адекватно относиться к сенсационным заявлениям вроде того, что британские учёные открыли во Вселенной и уже вовсю исследуют 21-е измерение (мы-то с вами тут и 4 измерения толком представить не можем!). Благородное требование честности и неподкупности науки в буржуазном обществе невыполнимо. Как и всё остальное при капитализме, наука продаётся и покупается. Наука вместе с культурой, искусством и другими элементами идеологической надстройки, включая такие реакционные, как религия и оккультизм, активно используется правящим классом для «запудривания» мозгов. И чтобы не быть сбитыми с толку показным наукообразием, нам следует самим на доступном широкому кругу трудящихся уровне разбираться в науке, имеющей не только прикладное, но и важное мировоззренческое значение. Так что добро пожаловать в теоретическую физику!
1. Работа
Когда в результате действия силы на тело оно приходит в движение, некоторая потенциальная энергия «источника силы» преобразуется в кинетическую энергию, эта последняя может быть частично или полностью рассеяна (то есть, преобразована в тепло).
Величина преобразованной энергии «источника силы» называется работой силы. Очевидно, что работа имеет размерность энергии, то есть может быть измерена в тех же единицах, что энергия, например, в джоулях. Работа A в простейшем случае постоянной силы F, действующей на прямом пути l в том же направлении, в котором движется тело, равна произведению силы и пути:
A = Fl (5.1)
(здесь и далее первое число в нумерации формул будет означать номер выпуска наших бесед, где эта формула появилась).
В случае переменной силы, работа равна интегралу силы по пути:
A = ∫F(l)dl (5.1а)
2. Первая идея Лагранжева формализма (обобщённые координаты)
Первая замечательная идея лагранжева формализма (то есть, восходящего к Ж. Л. Лагранжу формально-аналитического метода решения физических задач) – обобщение уравнения (5.1).
Смысл обобщения таков: аналогичное уравнение можно составить, если вместо пути l выбрать какую-нибудь другую величину – «обобщённую координату» q, характеризующую «пространственную протяжённость» (например, площадь, объём или угол поворота, а также, например, массу, электрический заряд и даже энтропию, перетекающие «с одного уровня на другой»), а вместо силы F – «обобщённую силу» Q, величину, имеющую характер напряжённости, такую, чтобы произведение обобщённой силы и приращения соответствующей обобщённой координаты выражало работу:
A = ∫Q(q)dq (5.1б)
Размерность работы в любом случае, независимо от размерностей обобщённой силы и обобщённой координаты одинакова.
Для примера приведём несколько простых, но разнообразных случаев, когда работа выражается через обобщённую силы и приращение соответствующей обобщённой координаты. Простота примеров в том, что относятся они к «одномерным» случаям, точнее, системам с 1 степенью свободы, то есть, системам, описываемым функцией одной переменной, одной обобщённой координаты:
1. A = ∫F(l)dl
2. A = ∫σ(S)dS
3. A = ∫M(φ)dφ
4. A = ∫P(V)dV
5. A = ∫mg(h)dh
6. A = ∫U(q)dq
7. A = ∫T(S)dS
А если, кроме того, обобщённая сила постоянна, то формулы становятся совсем простыми, работа выражается простым произведением силы и координаты вместо интеграла силы по координате:
1. A = Fl l (сила х путь)
2. A = σS (коэфф. пов. натяжения х площадь)
3. A = Mφ (момент силы х угол поворота)
4. A = PV (объём, перетекающий по трубе)
5. A = (gh)m (масса в потенциальном поле)
6. A = Uq (разность потенциалов х перетекающий заряд)
7. A = TS (разность температур х перетекающая энтропия)
В 1-м примере обобщённой координатой является длина пути, но пути вдоль произвольной траектории, а обобщённой силой – проекция силы на траекторию. Такая «обобщённая координата» естественным образом использовалась ещё «на уровне начальной школы» , только не при вычислении работы по силе и пути, а при вычислении пути по скорости и времени движения путника по заданной траектории, по некой тропинке.
В последних четырёх примерах обобщённую силу можно интерпретировать как «разность потенциалов» (разность давлений, потенциалов поля тяжести, потенциалов электрического поля или температур) и работа совершается в результате «перетекания» с верхнего потенциала на нижний чего-то, характеризуемого соответствующей обобщённой координатой (объёмом, массой, электрическим зарядом, энтропией). Кстати, в бессмертном трактате Карно «о движущей силе огня…» теплород, перетекающий из одного резервуара в другой – и есть та самая энтропия.
Уже эти простые примеры весьма ценны. Во всех этих примерах, как и в случае обычной силы, в результате действия обобщённой силы на обобщённую координату происходит преобразование потенциальной энергии «источника силы» в другие формы.
Этого не происходит, если несмотря на наличие обобщённой силы (или разности потенциалов, не равной нулю) обобщённая координата не меняется (то есть, её приращение равно нулю) вследствие наличия потенциального барьера.
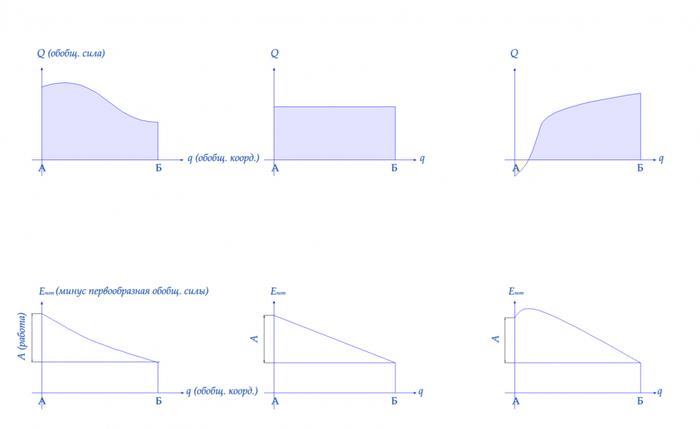
Сказанное можно проиллюстрировать геометрически. Величина работы численно равна площади под графиком Q(q). В случае постоянной силы это просто площадь прямоугольника.
Определённый интеграл функции одной переменной по формуле Ньютона-Лейбница равен разности значений первообразной в конечной и начальной точках. Минус первообразная обобщённой силы по обобщённой координате в данных одномерных случаях – это ни что иное, как потенциальная энергия.
Потенциальный барьер в этом случае наглядно изображается подъёмом графика потенциальной энергии выше начальной точки «А» (мы предполагаем, что кинетическая энергия в этой точке равна нулю)
При этом, как было сказано, преобразование энергии не идёт. Но мы можем вместо барьера поставить, так сказать, «канал сопряжения» (то есть, устроить так, чтобы приращение обобщённой координаты пошло по некоторому «каналу» и преобразование потенциальной энергии источника было сопряжено не с бесполезным рассеянием, а с совершением полезной работы). Мы можем заставить массу воды при падении с высоты, то есть, при преодолении разности потенциалов силы тяжести крутить турбины электростанции или можем заставить энтропию, перетекающую из камеры сгорания в окружающую среду, крутить двигатель автомобиля. Да и сама природа жизни заставляет потенциальную энергию, содержащуюся в белках, жирах и углеводах пищи, прежде, чем они окислятся до углекислого газа и воды, совершить разнообразную полезную для организма работу.
А ещё мы можем провести процесс в обратном направлении (против обобщённой силы), (тем самым накачав систему потенциальной энергией) затратив на это (за вычетом потерь) столько же энергии, сколько выделяется при протекании процесса в прямом направлении. Например, мы можем перекачать электрический заряд против разности электрических потенциалов, заряжая аккумулятор или перекачать энтропию от холодного тела к тёплому, увеличив тем самым разность температур между холодильной камерой и окружающей средой.
3. Выход в другие измерения
Напомню, что пока мы рассматривали «одномерные» случаи. В «одномерном» случае, то есть, при наличии у рассматриваемой физической системы лишь 1 степени свободы, форма пути между 2 точками фиксирована, дифференциал функции одной переменной, если можно так выразиться, всегда полный, значит, элементарная работа
δA = F(x)dx
– полный дифференциал, поэтому в одномерном случае суммарную работу на пути из точки А в точку Б всегда можно вычислить по формуле (5.1б)
A=∫Q(q)dq (5.1б)
Теперь вспомним, что мы живём в трёхмерном физическом пространстве. В нём одна материальная точка имеет три степени свободы, то есть, положение её описывается тремя координатами и обычная механическая сила, действующая на неё – величина векторная, имеющая три компоненты. Работа силы в трёхмерном пространстве подобно тому, как это было в одномерном случае, может быть вычислена по значениям первообразной от силы в 2 точках А и Б тогда и только тогда, когда работа на пути от точки А до точки Б полностью определяется 2 точками – точками начала и конца пути и не зависит от формы пути.
A = ∫d(-E_пот) = E_пот_1 — E_пот_2

Это бывает в том случае, когда элементарная работа
δA = Fx(x, y, z)dx + Fy(x, y, z)dy + Fz(x, y, z)dz (5.2)
является полным дифференциалом некой функции, иначе говоря, когда сила является градиентом некой скалярной функции (силовой функции, или минус потенциальной энергии U = -E_пот:
δA = ∂U/∂x(x, y, z)dx + ∂U/∂y(x, y, z)dy + ∂U/∂z(x, y, z)dz = ∇U (5.2а)
В этом случае все компоненты вектора силы F (а их в трёхмерном пространстве 3) в каждой точке определяются лишь 1 скалярной функцией, потенциальной энергией E_пот. Такие силы называют потенциальными, таковыми являются, например, сила тяжести, сила упругости… Когда такой кунштюк сведения вектора к скаляру возможен, вычисление работы сводится к вычислению разности потенциалов. О том, когда такой кунштюк возможен, мы поговорим в беседе, посвящённой математической теории поля. Там мы подробнее разберём и упомянутые понятия «полный дифференциал» и «градиент». А сейчас мы убедимся, что рассматриваемый метод обобщённых координат и обобщённых сил весьма полезен вовсе не только в таких особых случаях. Вначале найдём универсальное выражение для обобщённой силы.
4. Выражение обобщенной силы
Рассмотрим некоторую обобщённую силу Qi. Пока представим, что это просто одна из компонент вектора обычной силы, компонента вдоль координаты qi, причём qi – это просто одна из декартовых координат (x, y или z). Если рассматриваемая сила Qi потенциальна, то она по определению равна минус производной потенциальной энергии по координате:
A = ∂U/∂qi = — ∂E_пот/∂q_i (5.3)
Если в системе нет трения, то сила вызывает изменение кинетической энергии:
Qi = d/dt(mv) = d/dt(∂mv^2)/2∂v = d/dt (∂E_кин/∂q`_i ) (5.4)
«Ку с точкой» q` означает, как принято, обобщённую скорость, то есть, производную обобщённой координаты qi по времени.
Если выполнены указанные условия (потенциальность силы и отсутствие трения), то из двух предыдущих уравнений мы получим это:
d/dt (∂E_кин/∂q`_i) — (∂E_пот/∂q_i) = 0 (5.5)
Если же на нашу систему действуют ещё какие-то внешние (активные) силы, то уравнение (5.5) становится неоднородным, то есть, в нём появляется не равная нулю правая часть:
d/dt (∂E_кин/∂q`_i) — (∂E_пот/∂q_i) = Qi_внеш непотенц (5.5а)
Мы вправе написать уравнение не относительно двух разных величин E_пот и E_кин, а относительно их разности
E_пот — Е_кин ≝ L (5.6, функция Лагранжа)
которая называется кинетическим потенциалом, функцией Лагранжа или лагранжианом L:
d/dt (∂L/∂q`_i) — (∂L/∂q_i) = Qi_внеш непотенц (5.7, уравнение Лагранжа)
Дело в том, что если мы напишем уравнение Лагранжа так:
d/dt (∂(E_пот — E_кин )/(∂(q`_i ))-∂(E_пот — E_кин )/(∂q_i) = Qi_внеш непотенц (5.7а)
и применим правило «дифференциал разности равен разности дифференциалов», получим вот что:
d/dt (∂E_пот/∂q`_i — ∂E_кин/∂q`_i) — (∂E_пот/∂q_i — ∂E_кин/∂q_i) = Qi_внеш непотенц (5.7б)
Обычно E_кин заисит только от скоростей q`i, но не координат qi, а E_пот – наоборот, зависит только от координат qi, но не скоростей q`i. Поэтому в первой скобке исчезает первое слагаемое, во второй – второе и мы получаем уравнение (5.5а). Но в случае обобщённых координат в общем случае никакое слагаемое не обязано быть равным нулю, поэтому уравнение Лагранжа (5.7) более универсально, чем уравнение (5.5а). В следующей беседе мы удивимся, насколько оно универсально. Собственно, только что приведённые рассуждения – это вовсе не вывод уравнения Лагранжа, а лишь вспомогательные рассуждения, помогающие понять, «что к чему», а в следующей беседе мы подойдём к этому уравнению с другой стороны.
А теперь напишем такое же по виду, как (5.7) уравнение, но уже относительно кинетической энергии E_кин:
d/dt (∂E_кин/∂q`_i) — ∂E_кин/∂q_i = Qi_внеш (5.8)
здесь Qi_внеш – уже суммарная, потенциальная и непотенциальная обобщённая сила, действующая на систему извне и вызывающая изменение параметра qi, так называемая «активная» («внешняя») сила. Это уравнение нам в этой беседе ещё пригодится.
___
Дорогие товарищи, давайте сделаем небольшой перерыв. Текст самой интересной, второй части пятого выпуска будет скоро опубликован. А видео Вы можете посмотреть уже сегодня:
